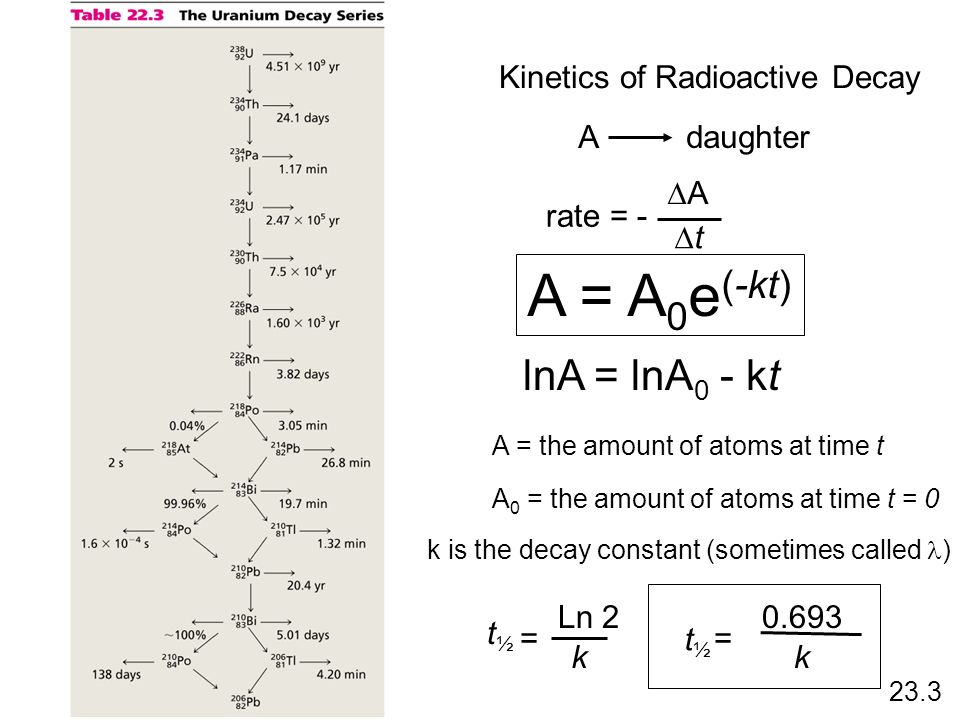
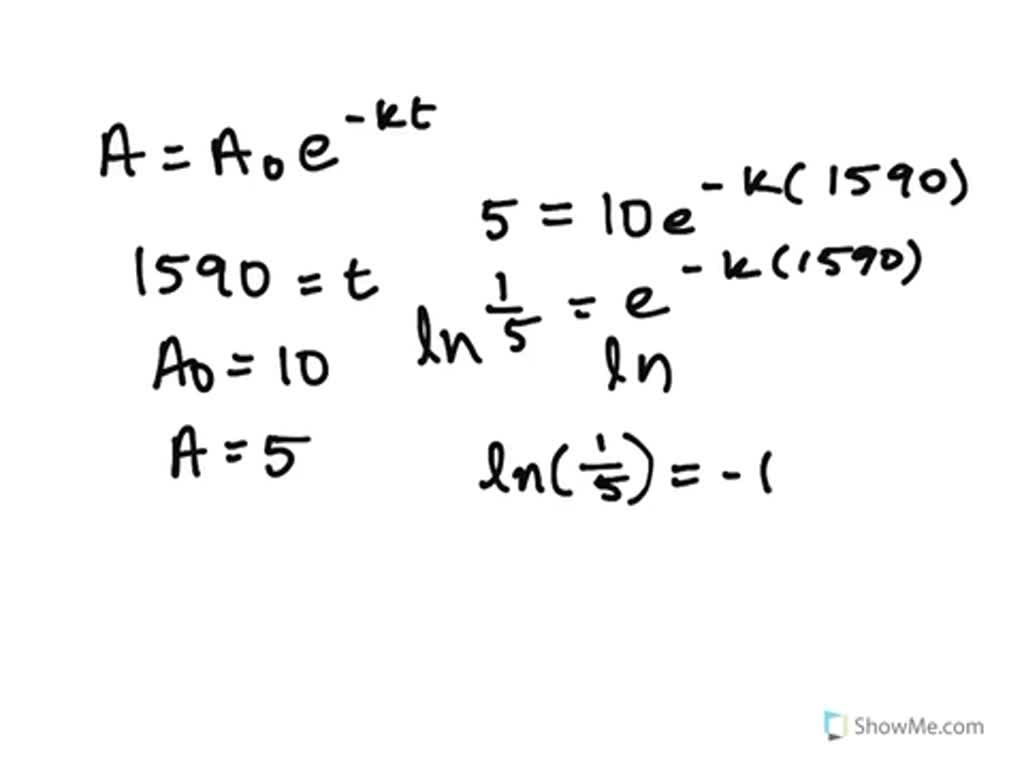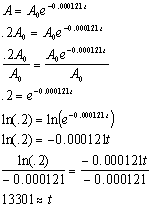PPT - Exponential Law: Uninhibited Growth: K > 0 Decay: K < 0 A = A o e kt PowerPoint Presentation - ID:1910479

PPT - Exponential Law: Uninhibited Growth: K > 0 Decay: K < 0 A = A o e kt PowerPoint Presentation - ID:1910479

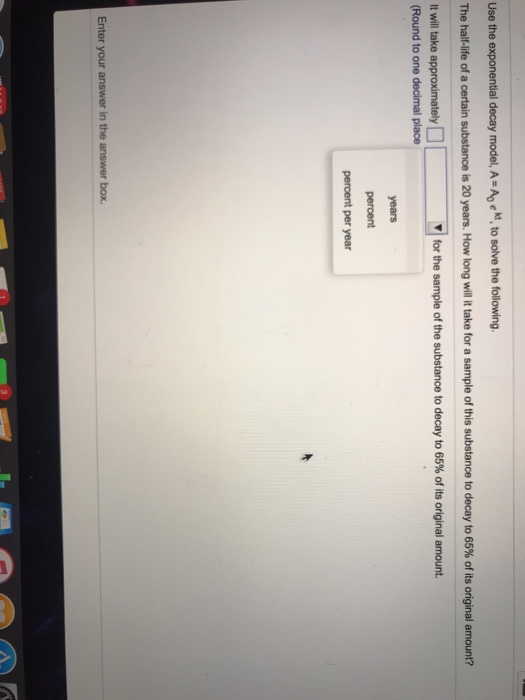
SOLVED: Use the exponential decay model, A=A0 e^k t, to solve Exercises 28-31 .Round answers to one decimal place. The half-life of lead is 22 years. How long will it take for

View question - Consider the radioactive decay formula A=Aoe^-kt where a is the amount of radium remaining at the time t. Ao is the amount present initially